Howto:Project 3D to 2D coordinates on desktop canvas

Goal

The goal of this article is to describe a method to project 3D geographical or cartesian coordinates to 2D screen coordinates using only Nasal language and camera properties exposed in the Property tree. The screen coordinates can be used further to position elements on the desktop canvas.

Use / Applications

The projection can be useful if you are intending to place canvas elements on the desktop canvas so that they are pointing towards an object in the 3D world. This task is required if you are intending to realize something like a mission or tutorial marker in 2D. This approach has the advantage of markers being always visible, independent of world geometry or clouds eventually occluding a similar marker in 3D. Projecting 3D to screen coordinates can also be useful to realize a HUD or overlay with pointers to airplanes and corresponding text information, if you want to create a virtual tower system or similar in Flightgear. Many applications are conceivable.

Solution sketch

Retrieving camera parameters from the property tree to reconstruct a projection and view matrix. Then using these matrices to transform a 3D coordinate to 2D screen coordinates.

Solution

Step 1

Find out the main window size and aspect ratio. The desktop canvas has the same size as the window and is always adjusted to it on resize. The property tree nodes "sim/startup/xsize" and "sim/startup/ysize" hold those values.

var screen_w=getprop("sim/startup/xsize");
var screen_h=getprop("sim/startup/ysize");
var aspect=screen_w/screen_h;

Step 2

Getting camera parameters to construct a perspective projection matrix.

The horizontal field of view (=fovx) in degrees is stored in "sim/current-view/field-of-view".

var fovx=getprop("sim/current-view/field-of-view")*D2R; 

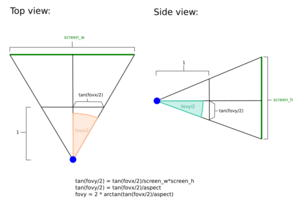
We convert it immediately to radians for further calculations. For the construction we do require the horizontal field of view (=fovy) though, which can be derived from fovx using some trigonometry.

var fovy = 2.0 * math.atan2(math.tan(fovx / 2.0) / aspect,1.0 );

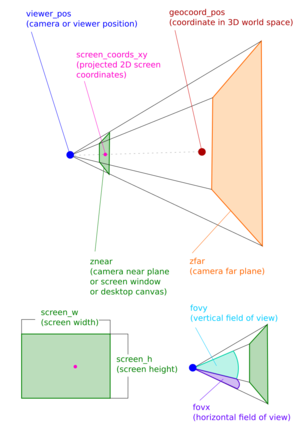
The camera near plane and far plane is stored in "sim/rendering/camera-group/znear" or "sim/rendering/camera-group/zfar" respectivly.

var znear=getprop("sim/rendering/camera-group/znear");
var zfar=getprop("sim/rendering/camera-group/zfar");

znear or zfar are distances from the viewer/camera position to the corresponding plane. 3D Geometry is rendered between those two planes. Rendering especially means projecting all 3D geometry onto the camera near plane which is analogous to our approach of solving the problem.

Step 3

By using the so far obtained camera information we can construct the perspective projection matrix like OpenSceneGraph is doing it for rendering Flightgear. The matrix is created like in the OpenGL function gluPerspective(). See https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluPerspective.xml for reference.

var create_projection_matrix_oglu = func(fovy, aspect, znear, zfar)
{
  var f=1.0/math.tan(fovy/2.0);
  var zdiff=znear-zfar;
  
  return [f/aspect, 0.0, 0.0,                 0.0,
          0.0,      f,   0.0,                 0.0,
          0.0,      0.0, (zfar+znear)/zdiff,  2.0*zfar*znear/zdiff,
          0.0,      0.0,  -1.0,               0.0];
}

var proj_mat = create_projection_matrix_oglu(fovy, aspect, znear, zfar);

The create_projection_matrix_oglu() function simply returns a nasal vector (or list) with 16 elements representing the 4x4 projection matrix.

Step 4

Instead of constructing a view matrix now we go a slightly different but equivalent way. First we use the viewer position and our 3D coordinate to form a differential vector like in the following.

var geocoord_pos = geocoord.xyz(); # our 3D coordinate, 
 				    # we want to project to screen
				    # geo.Coord class (see geo.nas) 
				    # xyz() converts to cartesian coordinates  in meters

var viewer_pos = [getprop("sim/current-view/viewer-x-m"), 
		   getprop("sim/current-view/viewer-y-m"), 
		   getprop("sim/current-view/viewer-z-m")]; # the position of the camera / viewer

var diff_vec = [geocoord_pos[0]-viewer_pos[0], 
		 geocoord_pos[1]-viewer_pos[1], 
		 geocoord_pos[2]-viewer_pos[2]]; # = geocoord_pos -  viewer_pos

The vector diff_vec then holds the position of the 3D coordinate relative to the camera. Now we need to rotate that vector into the camera space. We use a quaternion instead of a matrix for that task. The camera rotation quaternion can be fetched from the property like that:

var quat_viewer_rot = [getprop("sim/current-view/raw-orientation[0]"), 
			getprop("sim/current-view/raw-orientation[1]"), 
			getprop("sim/current-view/raw-orientation[2]"),
 			getprop("sim/current-view/raw-orientation[3]")];

To transform diff_vec with the quaternion quat_viewer_rot we use a function called rot_vec3_by_quat(), which will explained later.

var vec_view_space=rot_vec3_by_quat(diff_vec,quat_viewer_rot);

The result vector vec_view_space is now in camera space and ready for projection. We just add a fourth component to the vector in order to make it compatible with 4x4 projection matrix.

append(vec_rel_to_view,1.0);
 

Step 5

The projection of the 3D coordinate from camera space onto the near plane (screen) can be done by multiplying the projection matrix proj_mat with the vector vec_rel_to_view. Again we use a self made function called mat_vec_mult() for that task explained later.

var vec_proj=mat_vec_mult(proj_mat,vec_rel_to_view);

Afterwards the so called W-Clip should be done to get the final projected vector.

var device_coords_xy = [vec_proj[0]/vec_proj[3],
			 vec_proj[1]/vec_proj[3]];

As result we got a vector in device coordinates. The x and y component of that vector lies between -1 and +1 each. To transform this range to lie between 0 and 1 we do the following:

var norm_coords_xy = [(device_coords_xy[0]+1.0)*0.5,
		       (device_coords_xy[1]+1.0)*0.5];

Now we can multiply with screen size and have our final screen coordinates. Note in OpenGL coordinate system the Y axis is bottom to top, but in canvas coordinates we need Y to be from top to bottom.

var screen_coords_xy = [(norm_coords_xy[0]*screen_w,
			 (1.0-norm_coords_xy[0])*screen_h];

One more thing, the projection also works if the 3D coordinate lies behind the camera. To find out if it lies behind you can do this:

var is_behind = vec_view_space[2]>0.0;

Note that in OpenGL camera space negative Z values lie in front of the camera.

Appendix quaternions

To represent a quaternion we use a 4 element nasal vector.

var q=[w,x,y,z];

To calculate the conjugate quaternion of a quaternion q we use:

var quat_conj = func(q)
{
  return [q[0],-q[1],-q[2],-q[3]];
}

Multiplicating two quaternions (hamilton product) can be done with the following function:

var quat_mult = func(q1,q2)
{
    return [q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3],
            q1[0]*q2[1] + q1[1]*q2[0] - q1[2]*q2[3] + q1[3]*q2[2],
            q1[0]*q2[2] + q1[1]*q2[3] + q1[2]*q2[0] - q1[3]*q2[1],   
            q1[0]*q2[3] - q1[1]*q2[2] + q1[2]*q2[1] + q1[3]*q2[0]];
}

Rotating a 3 component vector with a quaternion q is defined by the function rot_vec3_by_quat().

var rot_vec3_by_quat = func(v,q)
{
    #rotate 3 component vector by quaternion
    var qv = [0, v[0], v[1], v[2]];
    var qr=quat_mult(quat_mult(q,qv),quat_conj(q));
    return [qr[1], qr[2], qr[3]];
}

Appendix matrix vector multiplication

Multiplying a 4x4 matrix with a 4 component vector is shown in the following mat_vec_mult() function. m must be a nasal vector (list) of 16 values and v a vector with 4 values.

var mat_vec_mult = func(m,v)
{
  var sm=size(m);
  var sv=size(v);
  if(sm==16 and sv==4)
  {
    return 
      [
      m[0]*v[0] + m[1]*v[1] + m[2]*v[2] + m[3]*v[3] ,
      m[4]*v[0] + m[5]*v[1] + m[6]*v[2] + m[7]*v[3] ,
      m[8]*v[0] + m[9]*v[1] + m[10]*v[2] + m[11]*v[3] ,
      m[12]*v[0] + m[13]*v[1] + m[14]*v[2] + m[15]*v[3]
      ];
  }

  die("Unsupported matrix/vector size.");
}

Limitations

The approach is working in a single window scenario. No guarantees for multi screen applications. If you want to use this approach in real-time, bear in mind that the properties we retrieved our camera parameters from are not updated frequently enough to ensure a fluent behavior. While it is possible to do so you should expect jittery results during camera/view changes.

Full source code to the solution

var mat_vec_mult = func(m,v)
{
  var sm=size(m);
  var sv=size(v);
  if(sm==16 and sv==4)
  {
    #4x4 matrix multiplied by 4 component vector
    return 
      [
      m[0]*v[0] + m[1]*v[1] + m[2]*v[2] + m[3]*v[3] ,
      m[4]*v[0] + m[5]*v[1] + m[6]*v[2] + m[7]*v[3] ,
      m[8]*v[0] + m[9]*v[1] + m[10]*v[2] + m[11]*v[3] ,
      m[12]*v[0] + m[13]*v[1] + m[14]*v[2] + m[15]*v[3]
      ];
  }
  die("Unsupported matrix/vector size.");
}

var quat_conj = func(q)
{
  #quaternion conjugate
  return [q[0],-q[1],-q[2],-q[3]];
}

var quat_mult = func(q1,q2)
{
    #quaternion multiplication, hamilton product
    return [q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3],
            q1[0]*q2[1] + q1[1]*q2[0] - q1[2]*q2[3] + q1[3]*q2[2],
            q1[0]*q2[2] + q1[1]*q2[3] + q1[2]*q2[0] - q1[3]*q2[1],
            q1[0]*q2[3] - q1[1]*q2[2] + q1[2]*q2[1] + q1[3]*q2[0]];
}

var rot_vec3_by_quat = func(v,q)
{
    #rotate 3 component vector by quaternion
    var qv = [0, v[0], v[1], v[2]];
    var qr=quat_mult(quat_mult(q,qv),quat_conj(q));
    return [qr[1], qr[2], qr[3]];
}

var create_projection_matrix_oglu = func(fovy, aspect, znear, zfar)
{
  # perspective projection matrix like in gluPerspective
  # fovy must be in radians
  var f=1.0/math.tan(fovy/2.0);
  var zdiff=znear-zfar;
  
  return [f/aspect, 0.0, 0.0,                 0.0,
          0.0,      f,   0.0,                 0.0,
          0.0,      0.0, (zfar+znear)/zdiff,  2.0*zfar*znear/zdiff,
          0.0,      0.0,  -1.0,               0.0];
}



#input is a coordinate created with geo.Coord class (see geo.nas)
var geo_unproject_to_screen = func(geocoord)
{
  var screen_w=getprop("sim/startup/xsize");
  var screen_h=getprop("sim/startup/ysize");
  var aspect=screen_w/screen_h;
  
  var fovx=getprop("sim/current-view/field-of-view")*D2R;#in radians
  var fovy = 2.0 * math.atan2(math.tan(fovx / 2.0) / aspect,1.0 );
  
  var znear=getprop("sim/rendering/camera-group/znear");
  var zfar=getprop("sim/rendering/camera-group/zfar");
  
  var proj_mat = create_projection_matrix_oglu(fovy, aspect, znear, zfar);
  
  
  var geocoord_pos = geocoord.xyz();
  var viewer_pos = [getprop("sim/current-view/viewer-x-m"),
			  getprop("sim/current-view/viewer-y-m"),
			  getprop("sim/current-view/viewer-z-m")];
  
  var diff_vec = [geocoord_pos[0]-viewer_pos[0],
			geocoord_pos[1]-viewer_pos[1],
			geocoord_pos[2]-viewer_pos[2]];

  var quat_viewer_rot = [getprop("sim/current-view/raw-orientation[0]"),
       		       getprop("sim/current-view/raw-orientation[1]"),
				 getprop("sim/current-view/raw-orientation[2]"),
				 getprop("sim/current-view/raw-orientation[3]")];
  
  var vec_view_space=rot_vec3_by_quat(diff_vec,quat_viewer_rot);
  append(vec_view_space,1.0);
  
  var vec_proj=mat_vec_mult(proj_mat,vec_view_space);
  
  var device_coords_xy = [vec_proj[0]/vec_proj[3],
				  vec_proj[1]/vec_proj[3]];

  
  var norm_coords_xy = [(device_coords_xy[0]+1.0)*0.5,
                        (device_coords_xy[1]+1.0)*0.5];
  
  var screen_coords_xy = [norm_coords_xy[0]*screen_w, 
				  (1.0-norm_coords_xy[1])*screen_h];
  
 
  return {screen_xy:screen_coords_xy,  is_behind: vec_view_space[2]>0.0};
}

Howto test

Testing the solution with a desktop canvas element is shown in the following example.

var coord = geo.Coord.new();
coord.set_latlon(51.124162,13.763609,300.0); # at EDDC airport
var marker = canvas.getDesktop().createChild("path", "marker")
        .move(-25,-50).line(50,0).line(-25,50).close()
        .setColorFill(1,0,0,1); # red triangle pointing 
					   # down to the 3D geo coordinate
 
var update=func()
{
  var proj_res=geo_unproject_to_screen(coord);
  marker.setTranslation(proj_res.screen_xy);
  marker.setVisible(!proj_res.is_behind);
}       
var update_timer=maketimer(0.04,update);#~25fps
update_timer.start();