JSBSim Aerodynamics

From wiki.flightgear.org

Jump to: navigation, search

JSBSim provides a framework for aerodynamics. This page will attempt to explain how to translate traditional aerodynamics concepts into the JSBSim framework, and how to create FDMs that are sane for any flight value.

This page uses the term "coefficient" both the traditional sense of a constant multiplicative factor or in the JSBSim sense of the output of a function derived from a coefficient.

Contents

Frames

JSBSim incorporates several frame of reference. The body frame and wind frame are the most important to the aerodynamic model.

  • Body XYZ The body frame uses the X axis for forward and aft, with + to the front. The Y axis is side to side with + to the right. The Z axis is up and down, with + being up. The origin of this frame is the Center of Gravity (CG), about which the aircraft forces and moments are summed and the resulting accelerations are integrated to get velocities.
  • Wind XYZ The wind frame X-axis points directly into the relative wind. The Y-axis is perpendicular to the X-axis, and remains within the aircraft body axis XZ plane (also called the reference plane). The Z-axis completes a right hand coordinate system. The origin of this frame is the AeroRP.
  • Wind UVW This isn't really a frame, but it is the components of the wind velocity vector. The relative wind is imposed on the body frame using variables U,V, and W. U to represent the velocity of the wind flowing past the aircraft. U represents the wind blowing down the X or longitudinal axis of the aircraft. V represents the wind blowing down the body frame Y axis, that is, wind in your ear. W represents wind blowing down the body frame Z axis, or wind from above.

Angles

These two angles define the direction the relative wind is blowing in regard to the body frame.

  • Alpha Alpha is the angle between the X body axis and the X wind axis measured on the UV plane. In standard aerodynamics Alpha is often referenced to the main wing chord line, this is not the case in JSBSim.
  • Beta Beta is the angle between the X body axis and the X wind axis measured in the UW plane.

QBar

QBar, or dynamic pressure, is the product of velocity^2*(air density)/2

  • QBarUV Use this value for formula involving Alpha. It is the value of QBar restricted to the vertical plane.
  • QBarUW Use this value for formula involving Beta. It is the value of QBar restricted to the horizontal plane.

Metrics

The metrics section provides a standard place to record common aircraft dimensions. Aeromatic built FDMs only use three of the defined properties.

  • Wing Area - metrics/Sw-sqft
  • Wing Span - metrics/bw-ft
  • Wing Chord - metrics/cbarw-ft

Other dimensions Aeromatic creates but does not use are: (tail arms are used by the JSBSim Turbulence code)

  • Horizontal Tail Area - Sh-sqft
  • Horizontal Tail Arm - lh-ft
  • Vertical Tail Area - Sv-sqft
  • Vertical Tail Arm - lv-ft

Forces

  • Lift: CL Lift is a function of QBar * Wing Area * Cllift. Cllift is generally derived from a 2D table as a function of AoA. In the real world it is also a function of Reynolds Number.
  • Drag: CD It is important to ensure all coefficient functions in the drag section remain positive. When drag coefficient functions are negative, drag is effectively acting as thrust opposite the relative wind.
  • Side: CY

Moments

  • Roll: Cl Aerodynamic rolling moment comes from multiple sources:
    • One is the lift generated by the vertical tail. On most aircraft the center of pressure for the vertical tail is not on the X body axis. This sets up a moment arm creating a moment of (moment arm length)*(vertical tail lift force).
    • Another roll moment source is main wing dihedral angle. FIXME: explain how dihedral contributes to roll moment.
  • Pitch: Cm The primary contributor to the pitching moment is the lift generated by the horizontal tail. The pitching moment of the main wing airfoil is a secondary contributor. Because of this fact it makes sense that the value for Cm will resemble the CL curve for the horizontal tail airfoil. The standard CL curve does not take into account the changes in tail Angle of Attack (AoA) and QBar due to main wing down-wash and rotational velocity around the Y axis. Using QBarUV is more appropriate for Cm than the generic QBar.
  • Yaw: Cn The primary contributor to the yawing moment is the lift generated by the vertical tail. The wind force on the fuselage is a secondary contributor. Because of this fact it makes sense that the value for Cn will resemble the CL curve for the vertical tail airfoil. Changes in QBar due to the vertical tail moving into the 'shadow' of a stalled main wing may need to be accounted for, as well. The source for vertical tail Angle of Attack (AoA) should be Beta and QBarUW is more appropriate for Cn than the generic QBar.

Effects

  • Stall - A 'stall' is generally regarded as a loss of lift due to flow separation over the top of a wing, however, examination of lift polar for an airfoil over a full 360 degrees shows that significant amounts of lift are NOT lost as the stall occurs. The biggest aerodynamic effect of a stall is a large and rapid increase in drag.
  • Spin - Spins are caused loss of stability in the Yaw Moment axis. A stock Aeromatic FDM yaw section does not take alpha into account when calculating the yaw moment.
  • Faking lift polars - If we assume a symmetrical airfoil that stalls at +/- 15 degrees (0.26 radians) AoA and assume the lift is linear between the two we can create a table like: 
<table >
 <independentVar lookup="row">aero/alpha-rad</independentVar>
 <tableData> 
   0.26  0.26
  -0.26 -0.26 
 </tableData>
</table>

Beyond +/- 22.5 degrees AoA we'll use 0.26 * sin(2*AoA) to approximate lift, and linear interpolate between 15 and 22.5 degrees AoA. (These numbers are rather arbitrary.) The resultant table returns the same value as alpha-rad for the "stable" flight regime so the function will accept the aeromatic coefficient. Outside of the "stable" flight regime a better number will be used allowing more realistic flight behavior at high alpha or beta angles. 

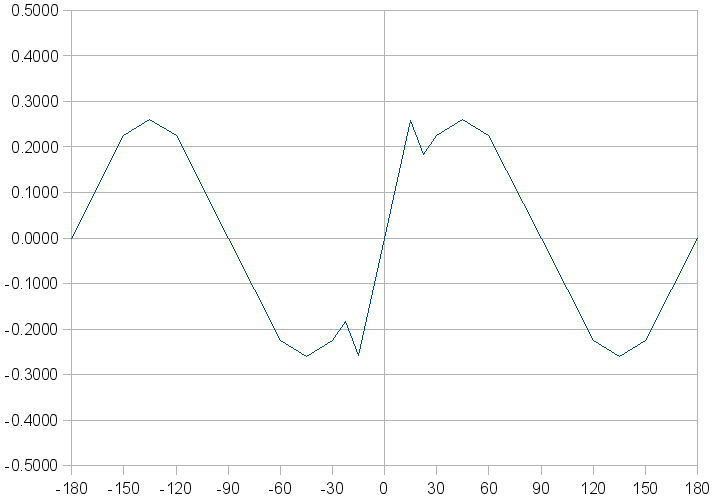
<table >
 <independentVar lookup="row">aero/alpha-rad</independentVar>
 <tableData> 
  -3.14   0.0
  -2.62   0.2252
  -2.36   0.26
  -2.09   0.2252
  -1.57   0.0
  -1.05  -0.2252
  -0.79  -0.26
  -0.52  -0.2252
  -0.39  -0.1838
  -0.26  -0.2588
   0.0    0.0
   0.26   0.2588
   0.39   0.1838
   0.52   0.2252
   0.79   0.26
   1.05   0.2252
   1.57   0.0
   2.09  -0.2252
   2.36  -0.26
   2.62  -0.2252
   3.14   0.0
 </tableData>
</table>

Image:fakelifttable.png

This table can drop directly into an aeromatic FDM to replace an instance of aero/alpha-rad or aero/beta-rad (changing the independent var of course).

  • Calculating Stall Speed - For an aircraft in straight and level flight, lift is equal to the weight of the aircraft. If we plug some numbers into the equation 
 lift = QBar * Sw-sqft * Cl

Using the Fi-156 Storch as an example 

 Weight = 2688 lb
 Wing Area = 280 sq-ft
 Stall Speed = 32 mph
 Air Density = 0.00238 slugs/ft^3
 QBar = 2.62871(slug ∕ (ft•s^2))

We get 

 2688 lb = 2.62871 (slug ∕ (ft * s^2)) * 280 ft^2 *Cl
 Cl = 2688 lbf / (2.62871 (slug ∕ (ft * s^2)) * 280 ft^2) = 3.65
Retrieved from "http://wiki.flightgear.org/index.php/JSBSim_Aerodynamics"
Personal tools